Preisverleihung des Dr. Hans Riegel-Fachpreises 2021
Die Carl von Ossietzky Universität Oldenburg und die Dr. Hans Riegel-Stiftung haben am 15.10.2021 die Dr. Hans Riegel-Fachpreise für besonders gute vorwissenschaftliche Arbeiten von Schülerinnen und Schülern aus Niedersachsen verliehen. Jedes Jahr werden circa 300 Schülerinnen und Schüler mit dem Dr. Hans Riegel-Fachpreis ausgezeichnet. Das Ziel des Dr. Hans Riegel-Fachpreises sei es, junge Talente auf ihrem Weg in ein naturwissenschaftliches Studium oder einen technischen Beruf zu begleiten, sagte Dr. Reinhard Schneider, Vorstandsvorsitzender der Stiftung.
Eine Experten-Jury der Universität Oldenburg bewertete die Arbeiten nach wissenschaftlichen Kriterien, wobei besonders kreative Themenstellungen sowie ein deutlich erkennbarer praktischer Eigenanteil (z. B. in Form von Experimenten) wichtige Einflussgrößen der Prämierung waren. Die Gewinnerinnen und Gewinner nahmen nun ihre Auszeichnungen stolz entgegen.
Nele Themann (MA 12) ist für ihre herausragende Facharbeit „Mathematisches Modellieren – Kubische Splinefunktionen und ihre Anwendung“ mit dem zweiten Platz ausgezeichnet worden.
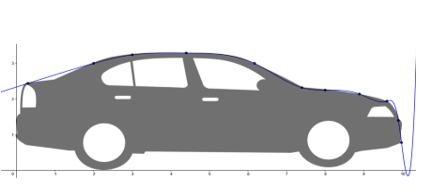
„Splines? Noch nie gehört, was soll das denn sein?“ Die Aufgabe besteht darin, den oberen, charakteristischen Umriss, z.B. der Karosserie eines Autos, nun möglichst genau mithilfe einer Funktion mathematisch zu modellieren, um mit dieser z.B. am Computer ein Modell zu erstellen und verschiedene statistische Berechnungen durchzuführen.
Erste Polynominterpolation:
f(x)= 0,01x^9 – 0,27x^8 + 3,96x^7- 36,64x^6+ 220,5x^5- 862,23x^4 – 2120,32x^3- 3030,44x^2+ 2105,32x – 407,25
Es ist zu erkennen (s. Abbildung rechts), dass die Funktion zwischen den Stützstellen zu stark ausschwingt und der Umriss des Autos auch nicht annähernd gut wiedergegeben wird.
Die Grundidee von Splinefunktionen besteht darin, dass statt eines einzigen Polynoms durch alle Stützpunkte bei der Spline-Interpolation eine Funktion gesucht wird, die aus stückweisen definierten Polynomen mit einem niedrigeren Grad zusammengesetzt ist.
Modellierung mithilfe der Spline-Interpolation:
Im Vergleich zu der Polynominterpolation stellt diese Modellierung mithilfe von kubischen Splinefunktionen eine bessere Annäherung an den tatsächlichen Umriss dar. Es ist zu betonen, dass die Oszillation im Vergleich zur Polynominterpolation deutlich geringer ausfällt und durch die abschnittsweise Definition auch nur in wenigen Intervallen zu beobachten ist.
Die Schulgemeinschaft gratuliert Nele recht herzlich für die tolle Leistung und wünscht Ihr auf dem weiteren Weg viel Erfolg und viel Freude!